I. Sesin Oluşumu ve Özellikleri

1.1. Ses Nedir?

Bir müzik notası ve genel olarak herhangi bir ses bir kaynaktan doğar, iletici bir ortam (genellikle hava) içerisinde yayılır ve bir alıcı (bir kulak veya bir mikrofon) tarafından algılanır. Bu yüzden kaynak, iletici ortam ve alıcı, akustik biliminin (müzik fiziği) üç temel öğesini oluşturur.

Öncelikle ses nedir? Sesten bahsederken, genelde havada dolaşan ve insan kulağı tarafından algılanabilen mekanik titreşimlerden bahsederiz. Bilim insanları, “sesin”, insan kulağı tarafından duyulmayacak kadar yüksek ve alçak frekanslara sahip olabilen ve gaz, sıvı ve katı olmak üzere her türlü maddi ortamda yayılabilen daha kapsamlı bir tanımını kullanırlar.

İster bir klarnetin sesi, ister çırpılan bir el sesi olsun, sesler her zaman bir kaynağın titreşimi sonucu oluşur. Çoğu zaman bu titreşimi fark etmek kolay değildir, özellikle el çırpması gibi sesin kısa ve keskin çıktığı durumlarda.

Sesin yayılabilmesi için iletici bir ortama ihtiyaç vardır. Ses dalgaları, ışık dalgaları gibi, boşlukta yayılamaz. İletici ortamı oluşturan parçacıklar (örneğin havadaki moleküller), ses kaynağına değme yüzeyinde, kaynağın yaptığı titreşime uyarak titreşmeye (ileri gidip gelmeye) başlarlar. Titreşmeye başlayan parçacıklar, kendi etraflarındaki diğer parçacıkları harekete geçirir, onlarda diğerlerini. Böylece hareket, zamanla birlikte giderek kaynaktan daha uzaktaki parçacıklara aktarılır. Sonuç olarak, ortamdaki parçacıklar hep denge konumları çevresinde hareket ediyor olmalarına rağmen, kaynağın titreşim enerjisi ortamda iletilir. Dikkat edilmesi gereken husus, ortamın ilettiği şeyin madde değil, enerji olduğudur.

Ortam içinde oluşan bu harekete ses dalgası diyoruz. Hava göz önüne alındığında, ses basınç dalgaları şeklinde yayılır. Su dalgasında dalga ilerlediği halde su yerinde kalırken ve yüzen nesne sadece yukarı aşağı hareket ederken, ses iletiminde de hava değil basınç iletilir. Ses dalgaları 20°C sıcaklıktaki havada saniyede yaklaşık 344 metre hızla ilerlemelerine karşın hava parçacıkları sadece birkaç mikron ileri ya da geri gider. Ortam içindeki parçacıklar, dalganın hareket yönüne paralel olarak titreşirler.

1.2. Sesin Temel Parametreleri

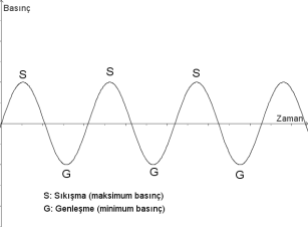
Sesin yayıldığı ortam içindeki bir noktada, basınç seviyesinin zamana göre değişimini bir detektör ile ölçebilir ve bu noktadaki zamana göre basınç değişimini çıkaran bir grafik oluşturabiliriz.

Şekil-1.

Titreşim sonucu oluşan basınç değişimleri yukardaki örnekte olduğu gibi belli bir zaman aralığı sonra kendini yineleyen bir karaktere sahipse, titreşim periyodiktir. Titreşimin periyodik olup olmaması, bir sesin nota veya gürültü olması arasındaki farkı belirler.

Şekil-2.

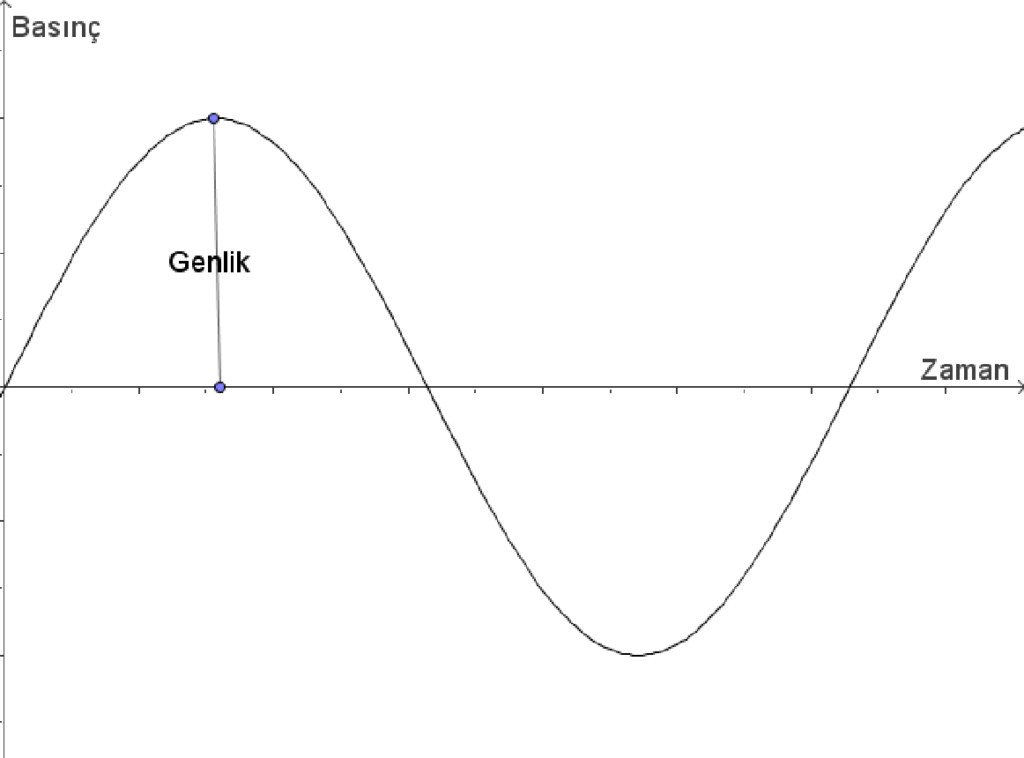
Basıncın x-ekseninin üzerinde (pozitif) olması o anda ölçüm yapılan noktada basıncın denge konumuna göre yüksek olması, altında (negatif) olması ise o anda o noktada basıncın denge konumuna göre düşük olması anlamına gelir. Bu grafiği, ölçüm yapılan noktadaki molekülün pozisyonunun denge konumuna göre zamana göre değişimi olarak da okuyabiliriz. Parçacığın denge konumundan uzaklığına genlik(amplitude) denir. Bazı durumlarda genlik deyimi kullanılırken kastedilen maksimum genliktir (şekil 3). Genlik sesin gürlüğünü belirler.

Şekil-3.

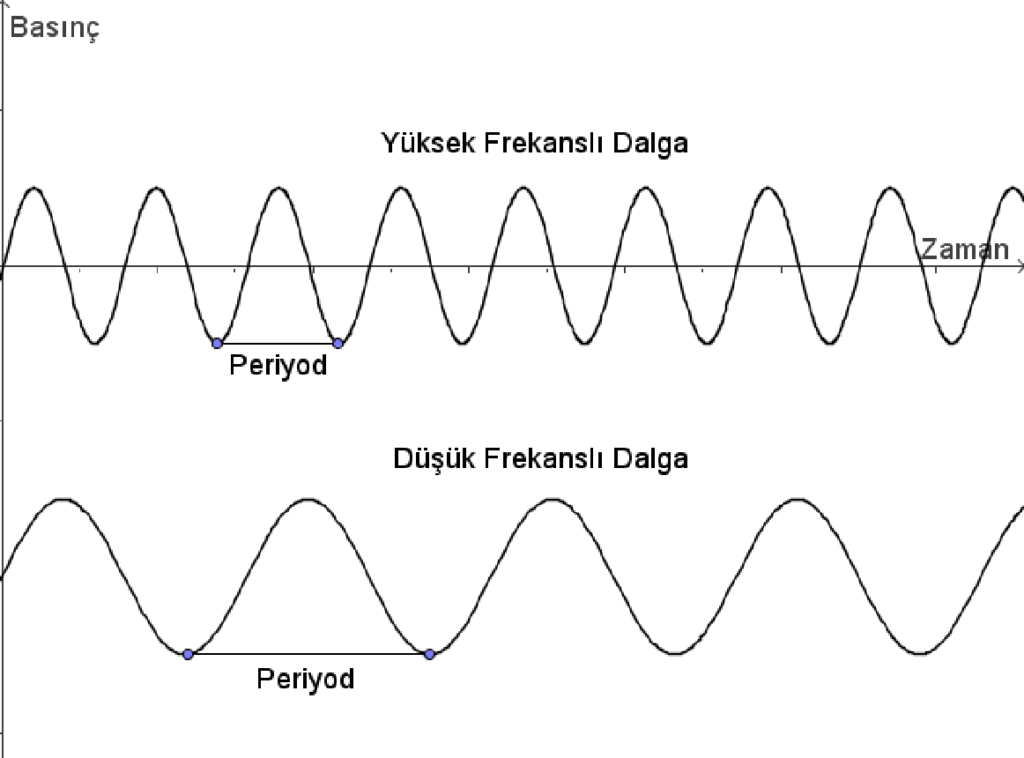
Periyod(T), tam bir salınım sırasında geçen zamanı belirtir. Frekans(f) ise belirli bir zaman diliminde kaç salınımın gerçekleştiğini belirler. Frekans ve periyod arasında basit bir ilişki vardır: f=1/T. Frekans için kullanılan standart birim Hertz’dir (Hz). 1 Hertz, bir saniyedeki titreşim sayısıdır. Örneğin, cisim saniyede 1000 kez titreşim yapıyorsa frekansı 1000 Hz olur.

Sesin hareketi sırasında ortam içindeki tüm parçacıklar aynı frekansla titreşir. Zira her parçacık komşusunun hareketi sonucu titreşir. Bu frekans aynı zamanda kaynağın da titreşim frekansıdır. 500 Hz ile titreşen bir kaynak, hava içerisindeki molekülleri de aynı frekansla titreştirir ve sonuç olarak kulağa gelen sesin frekansı da değişmez. Bir sesin frekansı, o sesin pes veya tiz olmasını belirler.

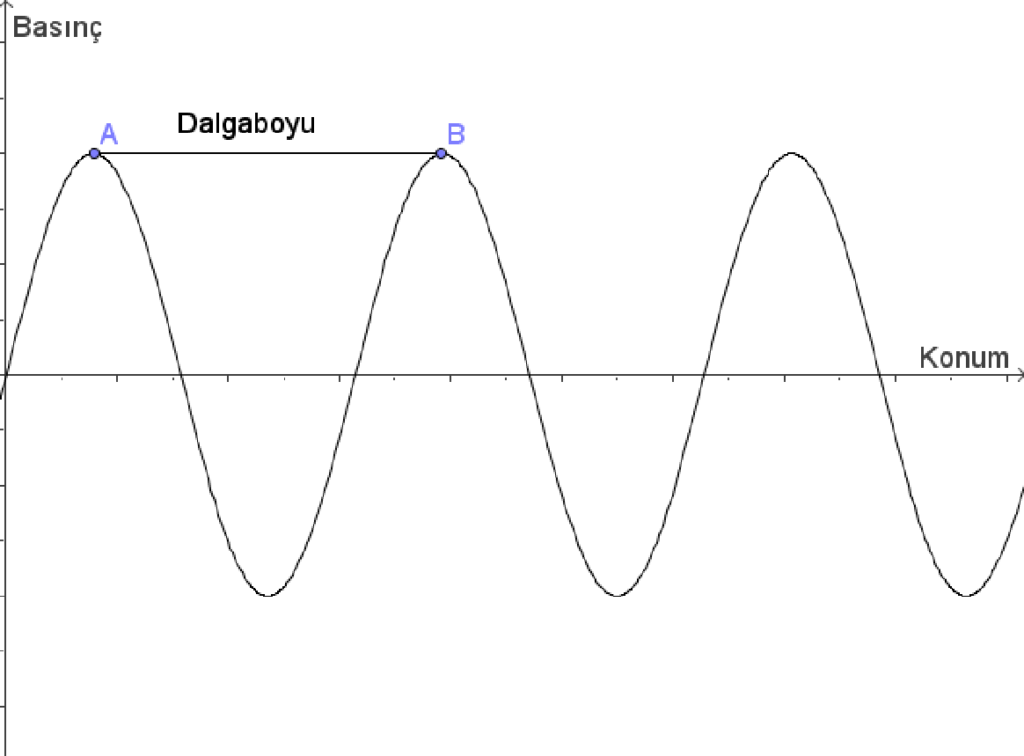
Şimdi de basınç-mesafe grafiğini ele alalım (yani zamanı donduralım). Durumu 1 boyutlu olarak ele aldığımızda karşımıza yine benzer bir grafik çıkacaktır. Bu grafikte iki tepe arasına dalgaboyu(L) denir. Başka bir deyişle dalgaboyu, dalganın bir salınımda kattetiği mesafedir.

Şekil-4.

Buna göre sesin hızı(v) için şu förmülü elde ederiz: v=Lf. Sesin hızını sabit olarak düşünürsek, sesin dalgaboyu ve frekansı arasında ters ilişki olduğunu görürüz.

1.3. Sesin Hızı

Sesin hızı, sesin frekansına (tiz veya pest olmasına) veya genliğine (kuvvetli veya zayıf olmasına) bağlı değil, sadece sesin içinde yayıldığı maddenin özelliklerine bağlıdır. Ses dalgalarının saf hava içerisinde yayılma hızı yaklaşık olarak bağıntısıyla elde edilebilir. Bu bağıntıya göre saf havada, ses dalgalarının hızı 0 oC’de 332m/s, 30 oC’de ise 350m/s yaklaşık değerlerini alır. Havaya su buharı, aşırı karbondioksit gibi yabancı gazların karışması bu katsayının değerininin değişmesine yol açar. Dolayısıyla, sıcaklıktaki değişim veya havadaki kirlenme nedeniyle sesin hızı değişir. Bu durum en çok üflemeli çalgıları etkiler, zira nefesli çalgıların titreşim periyodu sesin havadaki hızına bağlıdır. Dolayısıyla, hava ısınır veya kirlenirse çalgının frekansı değişir.

Çeşitli Ortamlarda (0°C de ) Sesin Yayılma Hızı (m/s)

Hava 332

Su 1454

Tahta 3828

Demir 5103

Taş 5971
 

Tablo-1.

Ses örneğin neden suda havadakine göre daha hızlı? Bunun sebebi, havayı oluşturan moleküller arasındaki mesafanenin daha büyük olmasından ve bu yüzden parçacıkların bir birini itmek için daha çok zaman harcamalarından kaynaklanıyor.

1.4. Ses Kaynaklarının Gücü

Ses kaynaklarının gücünden söz ederken, kaynağı ses verir hale getirmek için harcanan güç değil, kaynaktan yayılan sesin gücü, yani birim zamanda yayılan akustik enerji kastedilir. Bu ikisi, büyüklük bakımından çok farklıdır. Kaynaktan yayılan sesin gücünün, kaynağı ses verir hale getirmek için harcanan güce oranı, kaynağın ses verimini gösterir. Yaklaşık %1 verimle çalışan insan sesi en verimli çalgılardan biridir. Birçok çalgının ses verimi %1’in altındadır.

Fizikte, güç watt (W) cinsinden ölçülür. 1kg’lık bir kütleyi, 1 saniyede 1 metre öteye götürmek için harcanması gereken güce 1 watt denir.

Kaynaktan yayılan güç (P) doğal olarak kaynaktan uzaklaştıkça azalır. Genellikle ses kaynağından yayılan enerji her yöne doğru dağıldığı için, kaynaktan uzaklaştıkça dalga yüzeyi büyüyecek ve dolayısıyla birim yüzeye düşen enerji gitgide azalacaktır. Dağılmanın kabaca küre biçiminde olduğunu varsayarsak, kaynağın r birim uzağında, dalganın yüzeyi , birim yüzeye düşen güç ise kadar olur. Yani kaynağın bir metre ötesinde dalga şiddeti birim alan başına 1 birimken, 2 metre ötesinde birim alan başına ¼ birim olur.

Eğer, sesin azalmasında tek etken uzaklık olsaydı, o zaman bas seslerin nasıl olupta tiz seslere göre daha uzak mesafelere gidebildiğini açıklayamazdık. Bunun sebebi, ortamdaki moleküller arasındaki sürtünmeden kaynaklanan, enerjinin ortam içerisinde soğurulmasıdır. Sürtünme sonucu, dalganın bir kısmı ısı enerjisine dönüşür. Bu soğrulmayı etkileyen faktörler arasında, ortamın akmazlığı, özgül kütlesi, sıcaklığı, dalgaların ortam içerisindeki yayılma hızı ve en büyük ölçüde de dalgaların frekansı vardır. Hava ortamında, bir ses dalgasının 1m ilerlemesiyle soğrularak kaybedeceği dalga şiddeti frekansın karesi ile doğru orantılıdır. Buna göre, örneğin, 50Hz frekanslı bir ses ilerlerken, her metrede enerjisinin on milyonda birini kaybederken, 5000Hz frekanslı bir ses binde birini kaybedecektir. Dolayısıyla kaynaktan aynı güçle yayılan iki sesten 50Hz olanın rahatlıkla duyulabildiği uzaklıklarda, 5000Hz frekanslı olan belki de hiç duyulamayacaktır.

1.5. Ses Şiddeti Düzeyi

İnsan kulağı çok geniş bir aralıktaki ses şiddetini algılayabilir. Kişiden kişiye değişse de ortalama bir insanın, 1000Hz’lik bir ses için işitme eşiği , acı duyma eşiği ise kadardır. İki seviye arasındaki oran 1 trilyondur. İnsan kulağının bu kadar geniş bir aralık içindeki şiddetleri algılayabilmesi sebebiyle, ses şiddeti düzeyi(SŞD) (sound pressure level(SPL)) aşağıdaki fonksiyonla tanımlanır:

SŞD= 10 log(I/R) dB (desibel)1

Yani sesin mutlak şiddetinin(I) referans bir ses şiddetine (R) -ki R genelde işitme eşiğinin şiddeti olan değeri olarak alınır- oranının logaritması alınmıştır. Logaritma kullanılmasınının sebebi, bu sayede bağıl şiddetlerin çok daha dar bir alana sıkıştırılabilmesidir. (Logaritmalar sayılara göre çok daha yavaş artar. 10’un logaritması 1, 100’ün logaritması 2, 1000’in logaritması 3’tür) Bu fonksiyonun değeri bel(B) veya onun onda biri olan desibel(dB) cinsinden ifade edilir. Bir oranı ifade ettiği için dB boyutsuz bir birimdir.

Buna göre 0 dB (yani I= R olması durumu, log1=0), insan kulağının duyabileceği en düşük ses şiddetidir, ortamda ses olmaması anlamına gelmez. 85 dB üzerinde bir gürültü seviyesine uzun sure mahsur kalmak duyma bozukluğu gibi kulağa kalıcı hasar verebilir. 130 dB sınırının üzerindeki sesler ise insan kullağına ciddi acı ve kalıcı hasar verir. Aşağıdaki tablo çeşitli kaynakların ses şiddeti düzeyini desibel cinsinden vermektedir:

dB(SŞD)

 Kaynak (mesafeye bağlı olarak)

248

 Hiroşima ve Nagazaki’ye atılan atom bombaları

202-198

 İnsanın ses (şok) dalgasından ölümü

175.8

 80 m ötede patlatılan 1 Ton T.N.T.

164

 Büyük bir jet motorunun içindeki gürültü

154

 Oyuncak balonun ses yüzünden patlama sınırı

133

 Silah sesi

128

 İnsan saçının titreşimi hissetmeye başlaması

125

 Davul seti-vurma anında

116

 İnsan vücudunun pes frekansları hissetmeye başlaması

100

 Ortalama bir müzik setinin maximum sesi

60

 Normal konuşma

40

 Fısıltı

30

 Çölde tamamen sessiz bir gece

15

 1 m ötede 1 cm yükseklikten düşen iğne

0

 3 metre ötede bir sivri sinek

-30

 20 mil ötede konuşan bir insan

Tablo-2. (8)

1.6. Rezonans

İki duvar arasına gerilmiş bir tanbur telinin verdiği ses ile, tanburun üzerindeki telin verdiği ses arasında inanılmaz bir gürlük fark vardır. Bunun temel olarak üç nedeni vardır. Bunlardan birincisi, telin tek başına harekete geçirebildiği hava kütlesi çok küçüktür ve dolayısıyla havadan kulağa iletilebilen akustik enerji de az olur. İkinci neden ise, havanın titreşen tel etrafında yaptığı dolaşım hareketidir. Telin ileri doğru giderken sıkıştırdığı hava, düz bir şekilde ortam içinde yayılmak yerine, telin hemen arkasında oluşan düşük basınç bölgesine gitmeyi tercih eder. Tel geri dönerken de bu hava tekrar eski yerine dönmek ister. Dolayısıyla, ortam içinde yayılan akustik enerjinin büyük bir bölümü telin etrafında kalmış olur. Ama sesin gürlüğünü sağlayan en önemli neden, kuşkusuz çalgının gövdesinin telle rezonans haline girmesidir. Diğer nedenler rezonansın sağladığı güçlendirmenin yanında çok etkisiz kalır. Nedir rezonans?

Bütün çalgılarda bir uyarıcı sistem (ör. gitarın teli), bir de uyarıcı sistemin etkisiyle titreşen ve rezonatör (ör. gitarın gövdesi) denilen ikinci bir sistem vardır. Uyarıcı sistemin rezonatörü kendi frekansıyla titreşmeye zorlamasının, sesin gürlüğünün artmasını sağladığını söylemiştik.

Rezonatörlerin kendi öz frekansları vardır. Öz frekans, cismin dışardan bir uyarı aldığında yaptığı titreşimin frekansıdır. Uyarıcı sistemin frekansı ile rezonatörün öz frekansı aynı değerde ise, oluşan titreşimin genliği, uyarıcı sistemin genliğine göre çok büyük değerler alabilir. Bu olaya rezonans denir. Yani rezonans, bir rezonatörün, kendi öz frekansına uygun bir uyarıcıya gösteriği tepkidir. Örneğin bir soprano, cam bir kadehin öz frekansına uygun bir sesi yeterli bir şiddette çıkararak, kadehi parçalayabilir. Oysa, bir stadyum dolusu insan bütün güçleriyle bağırsa bile bu işi yapacak enerjiyi sağlayamaz.

Rezonatörlerin, seçimlilik parametreleri vardır. Rezonatörün seçimliliği büyükse, sadece belli frekanslardaki titreşimleri kuvvetlendirir; fakat çok kuvvetlendirir. Rezonatörün seçimliliği küçüldükçe daha çok sayıda frekansa tepki verir ama onları daha küçük oranlarda kuvvetlendirir. Ne tür rezonatör kullanılacağı, rezonatörün hangi amaçla kullanılacağıyla ilintilidir. Örneğin, radyo alıcıları, yüzlerce elektromanyetik titreşimi aynı anda alır. Alıcıdaki elektronik devreler, bu titreşimlerden her hangi biriyle seçimli rezonans yapmak üzere ayarlanabilir. Radyo örneğinde seçimliliği büyük olan bir rezonatör tercih edililir. Öte yandan örneğin çalgılarda, sesi güçlendiren parçaların seçimsiz rezonatör olması zorunludur. Yoksa çalgıda isteğimiz dışında kimi sesler çok gür, kimileri çok hafif çıkar.

Rezönatörler sadece sesin yüksekliğini arttırmakla kalmazlar, niteliğini de önemli ölçüde etkilerler.

II. FREKANS ANALİZİ

Doğadaki ses dalgaları çoğu zaman tek bir frekanstan değil, üst üste binmiş farklı frekanslara sahip birçok titreşimden oluşur. Bu durum sadece ses dalgaları için geçerli olan bir durum değildir. Örneğin bir ışık dalgası, içinde farklı yoğunluklara sahip birçok renkten (yani frekanstan) oluşur. Bir prizma kullanarak, ışık dalgasını kendini oluşturan basit renk frekanslarına ayırıştırabililiriz. Bu konuyu biraz sonra tekrar ele alacağız. Öncelikle dalgaların temel bir özelliğini incelememiz gerekiyor.

2.1. Ses Dalgalarının Girişimi

Ortam içinde ilerleyen iki dalga üstüste geldiği, oluşan bileşke dalganın genliği, ayrı ayrı dalgaların genliklerinin toplamı olur. Yani ses dalgaları girişimle birbirini kuvvetlendirip, zayıflatabilirler.

ÖRNEK 1

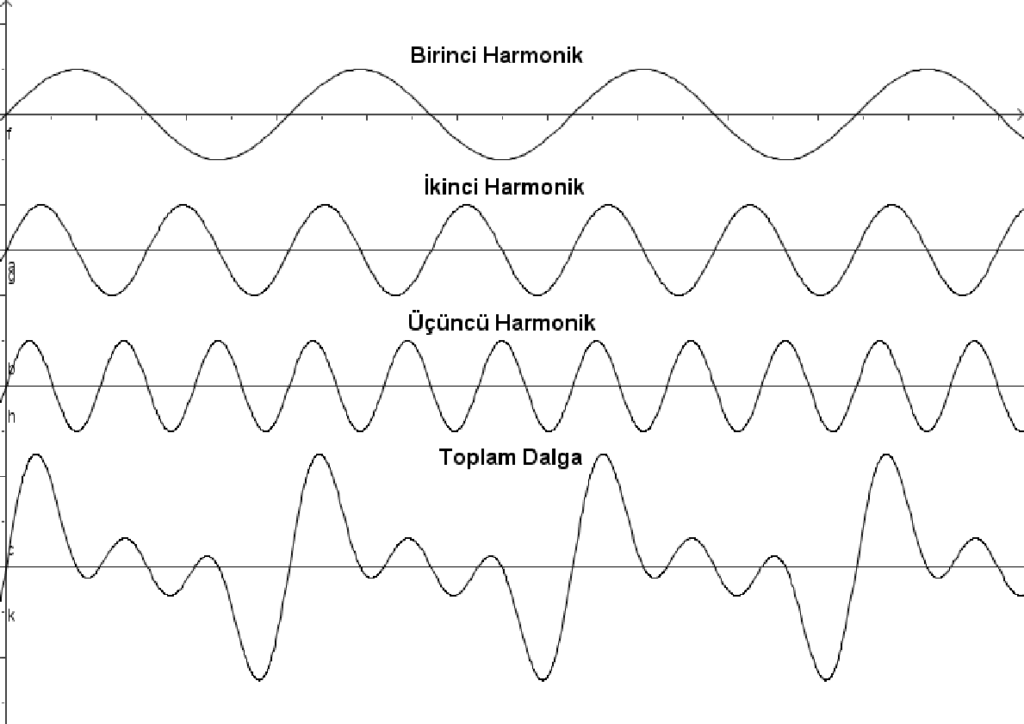
Aşağıdaki ilk üç ses üst üste binerek altıncı sesi oluşturur.

Şekil 5.

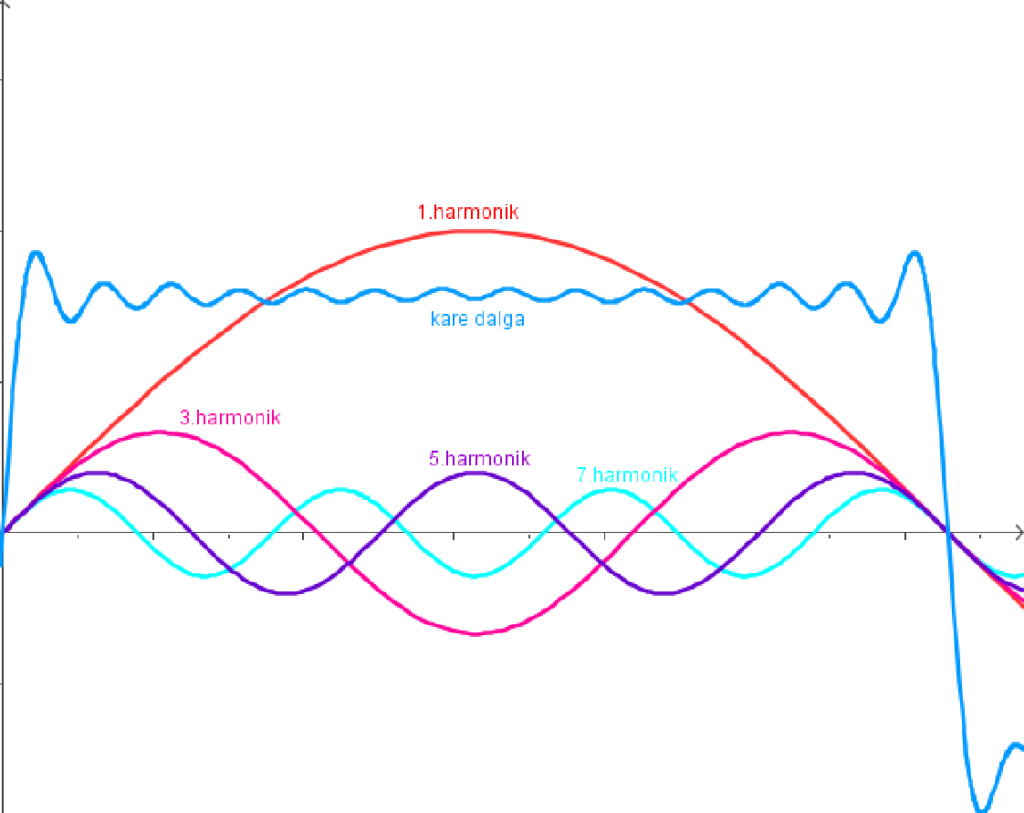
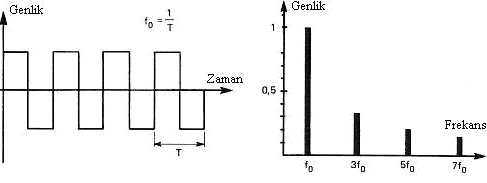
ÖRNEK 2: Kare dalga ve ilk dört bileşeni (1.-3.-5. ve 7. harmonikler)

Şekil 6.

2.2. Frekans Analizi

Yukardaki işlemin tam terside mümkündür. Yani karmaşık bir ses kendini oluşturan daha basit seslere ayrıştırılabilir. Fransız matematikçi Fourier, 1822’de, bir eğrinin ne kadar kompleks bir şekle sahip olursa olsun, bir dizi sinüs eğrisinin (saf sesler) toplamı olarak ifade edilebileceğini göstermiştir.

Fourier’in teoremi, periyodik olan herhangi bir eğrinin temel frekanslı (eğrinin frekansı) bir sinüs eğrisi, temel frekansın iki katı frekanslı bir sinüs eğrisi, temel frekansın üç katı frekanslı bir sinüs eğrisi şeklinde giden bir sinüs eğrileri dizisinin toplamı şeklinde yazılabileceğini söyler. Bu toplam sonsuza kadar gidebilir, ancak bu sinüs eğrilerinin genliklerinin sıfıra doğru gitmesi kaydıyla. Her frekansın yoğunluğuyla beraber gösterildiği grafiğe frekans spektrumu diyoruz.

Örnekler

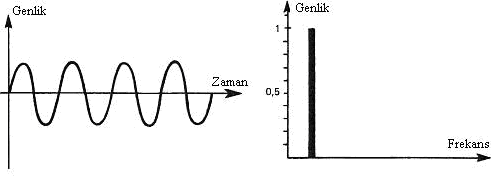
Aşağıdaki örneklerde birinci grafik, ortam içindeki bir parçacığın zamana göre denge konumuna uzaklığının nasıl değiştiğini (veya ortam içindeki bir noktadaki zamana göre basınç değişimini), ikinci grafik ise bu titreşimin frekansını göstermektedir.

ÖRNEK 1: Saf sinüs sinyali (basit ve periyodik)

Şekil 7. (4)

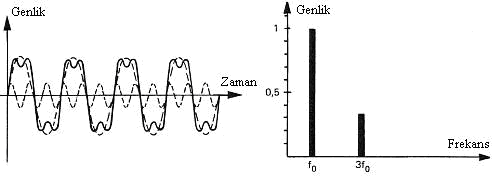
ÖRNEK 2: İki sinüs sinyalinin birleşimi

Şekil 8. (4)

ÖRNEK 3: Kare dalga (karmaşık ama periyodik)

Şekil 9. (4)

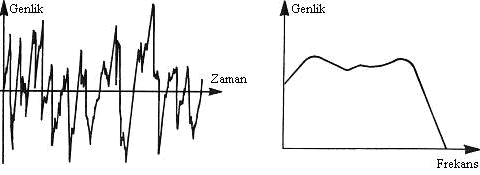
ÖRNEK 4: Rastgele sinyal (karmaşık ve peryodik değil)

Şekil 10. (4)

Her frekans kulağımızdaki belli bir bölgeyi uyaracaktır. Eğer ses dalgası içinde belli bir frekans baskın ise belli bir reseptör bölgesi daha belirgin olarak uyarılır ve sonuçta bir nota duyarız (örnek 1-2-3). Eğer gelen ses dalgası tüm reseptörlerimizi harekete geçirecek bir frekans skalasına sahip ise, duyduğumuz şeye bir gürültü deriz (örnek 4) . Eğer bir ses dalgasının spektrumu düz ise (her frekans eşit yoğunlua sahip ise), bu sese beyaz gürültü (white noise) deriz, aynı tüm görünür frekanslara eşit yoğunlukta sahip olan bir ışık dalgasının beyaz rengi oluşturması gibi.

2.3. Sesin Tınısı

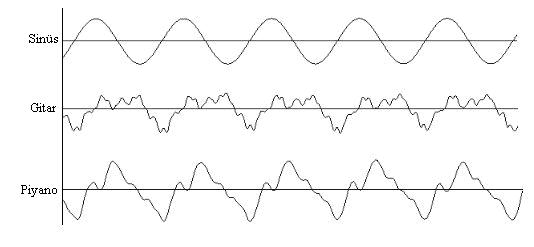
Şekil 11. (5)

Yukardaki ses dalgalarından en basiti olan örnek 1 bir bilgisayar tarafından üretilmiş saf sestir (pure tone). Görüldüğü üzere, “gerçek” enstrümanların çıkardıkları seslerin dalga yapıları çok daha karmaşıktır ve tek bir frekanstan oluşmazlar (örnek 2-gitar, örnek 3-piyano). Aynı anda farklı frekanslara sahip birden çok titreşim yaratırlar. Yukardaki şekilden görüleceği gibi üç sesin de temel frekansları aynıdır. Bu frekans aynı zamanda sesin notasını belirler. Bu frekansların kombinasyonu, enstrümanın tınısını belirler. Şimdi bir sesin nasıl olupta içinde birçok sesi barındırabildiğini inceleyelim.

2.4. Üstsesler: Harmonikler ve İnharmonikler

İki ucu sabitlenmiş bir teli düşünelim (örneğin bir gitar teli). Bu tel nasıl bir titreşim yapabilir? İlk olarak aşağıdaki gibi ileri-geri bir hareket yapabilir:

Şekil 12.

Veya telin her yarım veya üçte birlik parçasının komuşusuna göre ters yönde hareket ettiği daha kompleks biçimlerde titreşebilir:

Şekil 13.

Aslında, bir gitar teli, titreşimi sırasında yukarıdaki hareketlerin hepsini ve dahası sonsuz çoklukta diğerini aynı anda yapar. Her bir titreşim kendi frekansına ve genliğine bağlı basit bir basit ses oluşturur.

İlk örnekteki ileri-geri hareketin sonucu olarak oluşan basit dalganın frekansına temel frekans denir. İkinci moddaki titreşimin frekansı temel frekansın iki katıdır (yani bir tam oktav üstü). Üçüncü moddaki titreşimin frekansı ise temel frekansın üç katıdır (yani temel frekansın bir üst oktavdaki tam beşlisi). Temel frekansın tam katı olan bu basit dalgalara harmonik adı verilir. Doğal yollarla oluşan titreşimlerde, bu harmoniklerin sayısı teorik olarak sonsuzdur ve frekansları artarken genlikleri ise azalır.

Müzik enstrümanlarının sesleri analiz edilecek olursa, titreşimlerin her zaman tam olarak periyodik olmadığı görülecektir. Bir piyano sesinde oluşan üst sesler, harmonik seriden küçük bir farklılık gösterir, öte yandan bir çok perküsyonun frekans analizinde, bu enstrümanların harmoniklerden daha tiz veya daha pest üst sesler ürettikleri görülebilir. Üst seslerin tizliği veya pestliği, oluşan sesin tını diye nitelediğimiz karakterini belirler.

Üst sesler içerisinde, temel frekansın tam sayı katları olan frekanslara harmonikler (veya selenler), tam sayı katları olmayanlarına ise inharmonik üstsesler diyoruz.

İnharmonite arttıkça nota duyumuda kaybolmaya başlar. Cymbals, tam-tams ve chimes gibi bir çok perkusif enstrüman kompleks ve inharmonik sesler üretirler. Telli enstrümanlarda ise teller, kısaldıkça ve kalınlaştıkça inharmoniteleri de artar.

III. AKORT SİSTEMLERİ**

3.1. Aralık Bilgisi

İki nota arasında oluşan aralık, tiz sesin frekansının pest sesinkine oranıyla, yani tiz sesin pest sese göre bağıl frekansıyla belirlenir. Örneğin 300Hz ve 200Hz frekanslı iki ses arasında 3/2 iki oranı vardır. 300Hz’den 450Hz’e geçildiğinde de aynı aralık söz konusudur ve seslerin mutlak frekansları değişse bile eğer aralarındaki oran değişmiyorsa hep aynı aralık oluşur ve aynı müzik duygusu algılanır.

Bir aralığın büyüklüğünü ölçmek için çeşitli ölçüm birimleri kullanılır.

  1. Sent Aralığı: Sent denilen aralık, bir oktavı 1200 eşit parçaya bölerek elde edilir. Bu ölçü birimi, bir oktavın 12 eşit aralıktan oluştuğu tanpere müzik sistemi göz önüne alınarak geliştirilmiştir. Tanpere sistemdeki aralıklar şu şekilde ifade edilebilir:

Minor ikili (C-Db) = 100 sent Majör ikili (C-D) = 200 sent Minör üçlü (C-Eb) = 300 sent

vs…

  1. Koma Aralığı: Bir oktavı eşit 53 parçaya bölen birime Holder koması veya kısaca koma denir. Sekizliyi 53 eşit parçaya bölme düşüncesi, dizilerin doğal oluşumunda pratik bakımından son noktanın 53 sesli dizi olmasından kaynaklanmaktadır.

Yunan matematikçi Pisagor, kulağın hoşuna giden iki ses arasındaki aralığın bağıl frekansının 1/2 veya 2/3 gibi basit kesirli sayılardan oluşması gerektiğini söyler. Kesirler ne kadar küçük olursa, aralık o kadar uyumlu duyulur. Unison’dan (1/1) sonra, en uyumlu aralıklar, oktav (2/1), tam beşli (3/2), tam dörtlü (4/3), majör altılı (5/3), majör üçlü (5/4), minör üçlü (6/5),vs... Bu teoriye uygun bir şekilde Batlamyus tarafından geliştirildiği düşünülen doğal dizide (natural scale), ilk notanın frekansı sabitlendikten sonra, dizideki diğer notaların frekansları aşağıdaki tablodaki oranlarla ifade edilir.

 

C

D

E

F

G

A

B

C

1/1

9/8

5/4

4/3

3/2

5/3

15/8

2/1
 

Tablo-3. (7)

Diziyi dinlemek için tıklayınız.

Aslında, 1/1 ve 2/1 arasındaki her bir kesirli sayı, dizi içerisindeki potansiyel bir notayı işaret eder. Örneğin, Batlamyus’un dizisini genişleterek 12 sesli kromatik bir dizi elde edebiliriz:

 

C

C#

D

Eb

E

F

F#

G

Ab

A

Bb

B

C

1/1

16/15

9/8

6/5

5/4

4/3

45/32

3/2

8/5

5/3

9/5

15/8

2/1
 

Tablo-4.(7)

Kullanılacak nota sayısının 12 ile sınırlanmasına da gerek yoktur. 1588 yılında, birçok uyumlu akor kullanabilmek amacıyla, Gioseffo Zarlino aşağıdaki 16 notalı modeli kullanan bir klavsen geliştirmiştir:

 

C

C#

D-

D

Eb-

Eb

E

F

F#-

F#

G

G#

A

Bb-

Bb

B

C

1/1

25/24

10/9

9/8

32/27

6/5

5/4

4/3

25/18

45/32

3/2

25/16

5/3

16/9

9/5

15/8

2/1
 

Tablo-5.(7)

Diziyi dinlemek için tıklayınız.

İçindeki aralıkların kesirli sayılarla ifade edildiği ses dizilerine “just intonation” deniliyor. Bu tarz dizilerle bestelenen parçalardan örnekler:

. La Monte Young - The Well-Tuned Piano, dinle.

. Ben Johnston - Suite for Microtonal Piano (1977), dinle, (piyano tamamen do’nun üst seslerine göre akort edilmiştir)

. Kyle Gann - Custer and Sitting Bull , dinle (31 seslik bir dizi kullanılmaktadır.)

3.2. Doğal Dizinin sorunu: Transpozisyon

Aralıkların kesirli sayılarla ifade edildiği dizilerdeki en büyük sorun, yapılan müziğin transpoze edilememesidir. Bunun sebebini basit bir örnekle anlatmak gerekirse, örneğin C ve D notalarının birbirine oranı 9/8 iken, D ve E notalarının oranı (5/4)/(9/8) = 10/9 olur. Yani C-D aralığı ile D-E aralığı birbirinden (birbirine yakın olsalar da)farklıdır. Dolayısıyla, belli bir melodi dizide rasgele bir notadan başlayarak çalınamaz.

İkinci bir handikap ise dizideki bazı elemanların örneğin beşlilerinin bulunmamasıdır. Örneğin, ilk başta anlattığımız C sesinden başlayan doğal diziyi D sesini kök ses alarak çalalım (Dorian modu). Dinle

Dizinin kök sesi olan D’nin beşlisinin C’ye göre bağıl frekansı (9/8)(3/2)=27/16 olarak hesaplanır, oysa dizide C’ye göre bağıl frekansı bu oranda bulunan bir nota bulunmamaktadır. Bu orana en yakın olan oran 5/3 ile A’nın oranıdır. Tam beşli olmayan bu tarz aralıklara –bir uluma sesini andırması sebebiyle- kurt aralığı denmektedir. Önceki örnekte oluşan kurt beşlisini örnek1’i, gerçek bir 3/2 beşlisi ile kıyaslamak için ise örnek2’yi dinleyebilirsiniz.

3.3. Eşit Tanpereman

Bu sorunun üstesinden gelebilmek için, modern Batı müziği içinde eşit tampereman denilen sistem geliştirilmiştir. Bu sistemin gelişmesi ve büyük yaygınlık kazanması 17.yy’dan 20.yy’a kadar uzun bir zaman diliminde gerçekleşmiştir. Genelde, Bach’ın The Well-Tempered Clavier isimli kompozisyonunun bu sistem için yazıldığı düşünülür. Bach, gerçekten bir oktavı 12 parçaya bölmüştür ancak, bu aralıklar bugünkü kullandığımız aralıklar gibi eşit değil, biraz farklıydı. Bach’ın sisteminde herhangi bir ezgi mutlak bir şekilde transpoze edilemez ama sonuç oldukça makuldur. Bach’tan 19.yy sonuna değin klavyelerin akordu gitgide eşit tanpereman sisteme yaklaşmıştır. Ancak 1917’de tam bir eşit tamperemana izin verecek bir akort yöntemi geliştirebilmiştir.

Eşit tamperemanda, bir oktav, yarım ses denilen 12 eşit aralığa bölünür. Bu aralığın bağıl frekansının olması gerektiği gösterilebilir, yani yaklaşık olarak 1.059463. (Bu sayı aynı zamanda örneğin gitardaki iki ardışık perdenin uzunluklarınında oranıdır.)

Bu sistemin en büyük avantajı, mutlak bir transpoziyon olanağı sağlamasıdır. Ancak dezavantajları da barizdir; eşit tanpere edilmiş hiçbir sistemde unison ve oktav dışındaki doğal (Pisagoryen) aralıkların hiçbiri çalınamaz. (ispat: Bunun için 2m/12 = p/q denklemini sağlayacak m, p ve q tam sayıları var olmalıdır. Oysa kolayca gösterilebilir ki m=0, 12, 24,…. dışında bu denklemin çözümü yoktur. m’nin bu değerleri ise sırasıyla unison, birinci oktav, ikinci oktav,… aralıklarına karşılık gelmektedir.) Yani tanpereman sistemde, transpozisyon yapabilmek uğruna doğal aralıkları çalabilme yeteneğinden feragat edilmiştir.

Aşağıda, birinci tabloda doğal dizideki aralıkların sent karşılığı, ikinci tabloda ise 12 ton eşit tanpere sistemdeki seslerin, doğal dizideki eşlerinden hangi oranda saptığını görebilirsiniz:

 

Nota:

C

D

E

F

G

A

B

C

Oran:

1/1

9/8

5/4

4/3

3/2

5/3

15/8

2/1

Sent:

0

204

386

498

702

884

1088

1200
 

Tablo-6.(6)

 

Aralık

12 ton- eşit tanpere sistemdeki değeri

Doğal Dizideki değeri

Yüzde Farkı

Unison

20/12 =1.000000

1 = 1.000000

0.00%

Minör ikili

21/12 =1.059463

16/15 = 1.066667

−0.68%

Majör ikili

22/12 =1.122462

9/8 = 1.125000

−0.23%

Minör üçlü

23/12 =1.189207

6/5 = 1.200000

−0.91%

Majör üçlü

24/12 =1.259921

5/4 = 1.250000

+0.79%

Tam dörtlü

25/12 =1.334840

4/3 = 1.333333

+0.11%

Eksiltilmiş Beşli

26/12 =1.414214

7/5 = 1.400000

+1.02%

Tam Beşli

27/12 =1.498307

3/2 = 1.500000

−0.11%

Minör altılı

28/12 =1.587401

8/5 = 1.600000

−0.79%

Majör altılı

29/12 =1.681793

5/3 = 1.666667

+0.90%

Minör yedili

210/12 =1.781797

16/9 = 1.777778

+0.23%

Majör yedili

211/12 =1.887749

15/8 = 1.875000

+0.68%

Oktav

212/12 =2.000000

2/1 = 2.000000

0.00%
 

Tablo-7.(9)

Tanpere sistemdeki tam 5’li beşli aralık, doğal dizidekinden yaklaşık 2 sent daha pestir ki bu da birçok insanın algılayamacağı kadar küçüktür. İki sentlik bir aralığın nasıl duyulduğunu dinleyebilirsiniz: Dinle

Peki hangisi daha pes? (cevap: pes olan birincisi).

Öte yandan, tanpere dizideki majör üçlü, olması gerekenden duyulabilir oranda daha tizdir.

REFERANSLAR

  1. Ayhan Zeren, Müzik Fiziği, Pan Yayıncılık, 1995

  2. John Backus, The acoustical foundations of music, New York, Norton, 1977

  3. Arthur H. Benade, Fundamentals of musical acoustics, New York, Dover Publications, 1990

ONLINE REFERANSLAR

  1. John Perr, Temel Akustik ve Sinyal İşleme, http://www.turkuler.com/yazi/temelakustik.asp

  2. Yuval Nov, Explaining the Equal Temperament, http://www.yuvalnov.org/temperament/

  3. Kyle Gann, Just Intonation Explained, http://www.kylegann.com/tuning.html

  4. Kyle Gann, An Introduction to Historical Tunings, http://www.kylegann.com/histune.html

  5. William Hamby, Ultimate Sound Pressure Level Decibel Table, http://www.makeitlouder.com/Decibel%20Level%20Chart.txt

  6. Wikipedia, http://en.wikipedia.org/wiki/Equal_temperament

1 Alexander Graham Bell’in soyadıyla isimlendirilen desibel, bir oranı ifade ettiği için boyutsuz bir birimdir.

** Bu bölümdeki ses örnekleri Kyle Gann’ın “Just Intonation Explained” adlı sitesinden alınmıştır.